belajar matematika

Dalam rubrik pembahasan soal olimpiade kali ini, kita akan mencoba belajar tentang : menyelesaikan soal bilangan “ yang berderet “.

Kenapa judulnya bukan deret bilangan?

Karena tipe soal yang akan kita pelajari , bisa disederhanakan dan didekati dengan cara manipulasi bentuk (gak pake rumus deret).

Tipe soal macam ini sering kali muncul (khususnya pada tingkat seleksi kota), dengan tujuan (1) menguji kemampuan dalam mengenali pola dan (2) kemampuan memanipulasi bentuk aljabar. Yang keduanya merupakan syarat mendasar dalam mengerjakan soal olimpiade tingkat lanjut. Setidaknya kita akan mempelajari 2 bentuk dulu:

yang bisa disederhanakan dengan menyederhanakan pecahan
menggunakan bentuk identitas $\frac {1}{x.(x+1)}=\frac{1}{x}-\frac{1}{x+1}$ (bentuk yang penyebutnya merupakan perkalian bilangan berurut)

TIPE I:

Contoh 1:

Carilah nilai : $\left( {1 - \frac{1}{4}} \right)\left( {1 - \frac{1}{5}} \right)\left( {1 - \frac{1}{6}} \right)\,...\,\left( {1 - \frac{1}{{30}}} \right)$

Jawab :

Soal tipe ini biasanya lebih sederhana jika kita menyederhanakan bilangan-bilangan dalam tanda kurung.

Dan biasanya banyak suku akan saling menghilangkan.

Setelah disamakan penyebutnya, menjadi :

$\left( {\frac{3}{4}} \right)\left( {\frac{4}{5}} \right)\left( {\frac{5}{6}} \right)\,...........\,\left( {\frac{{29}}{{30}}} \right)$

Perhatikan bahwa penyebut pada suku ke-1 “dinetralisir” oleh pembilang pada suku berikutnya (menghasilkan angka 1— sebagai unsur identitas perkalian) , dan ternyata hal ini berlaku juga pada suku-suku yang lain:

= $\left(3\right)\left( {\frac{4}{4}} \right)\left( {\frac{5}{5}} \right)\,...........\,\left( {\frac{29}{29}} \right) \left( \frac{1}{30} \right)$

= $\frac{3}{{30}} = \frac{1}{{10}}$

Contoh 2: (Seleksi tingkat Kota 2003)

Berapakah hasil perkalian : $\left( {1 - \frac{1}{{2^2 }}} \right)\left( {1 - \frac{1}{{3^2 }}} \right)\left( {1 - \frac{1}{{4^2 }}} \right)\,...\,\left( {1 - \frac{1}{{2003^2 }}}\right)$ ?

Jawab :

$\left( {\frac{{2^2 - 1}}{{2^2 }}} \right)\left( {\frac{{3^2 - 1}}{{3^2 }}} \right)\left( {\frac{{4^2 - 1}}{{4^2 }}} \right)\,...\,\left( {\frac{{2003^2 - 1}}{{2003^2 }}} \right)$

$\frac{(2 - 1)(2 + 1)}{2.2}\rm{x}\frac{(3 - 1)(3 +1)}{3.3}\rm{x}..\rm{x}\frac{(2003 - 1)(2003 +1)}{2003^2 }$

$\frac{1\,.\,3}{2.2}\rm{x}\frac{2.\,4}{3.3}\rm{x}...\rm{x}\frac{2002\,\,\,2004}{2003.2003}$

$\frac{{1\,}}{2}\left( {\frac{3}{2}x\frac{2}{3}} \right)\left( {\frac{4}{3}x\frac{3}{4}} \right)\,\rm{x}...\rm{x}\left({\frac{{2003}}{{2002}}x\frac{{2002\,\,}}{{2003}}}\right)\rm{x}\frac{{2004}}{{2003}}$

$\frac{1}{2}\rm{x}\frac{2004}{2003} = \frac{2004}{4006}$

Tipe II

Contoh 3: (Seleksi tingkat Kota 2004)

Nilai dari $\frac{1}{2} + \frac{1}{6} + \frac{1}{{12}} + \frac{1}{{20}} + ..... + \frac{1}{{10100}}$ adalah….

Jawab :

Lihat penyebut, semuanya merupakan perkalian dari dua bilangan berurut.

Misal kita punya bilangan $\frac{1}{2}-\frac{1}{3}$ . Maka bisa kita sederhanakan menjadi $\frac{1}{2.3}$ . Atau sebaliknya, jika kita punya bentuk $\frac{1}{2.3}$ , bisa diubah menjadi $\frac{1}{2}-\frac{1}{3}$

Kembali ke soal.

Kita bisa mengubah bentuk soal menjadi :

$\frac{1}{2} + \frac{1}{{2.3}} + \frac{1}{{3.4}} + ..... + \frac{1}{{100.101}}$

Pecah menjadi pengurangan dua pecahan

$\frac{1}{2} + \frac{1}{2} - \frac{1}{3} + \frac{1}{3} - \frac{1}{4} +....+ \frac{1}{100} - \frac{1}{101}$

$\frac{1}{2} + \frac{1}{2} + \left( { - \frac{1}{3} + \frac{1}{3}} \right) + \left( { - \frac{1}{4} + \frac{1}{4}} \right) + ... + \left( { - \frac{1}{{100}} + \frac{1}{{100}}} \right) - \frac{1}{{101}}$ = $\frac{{100}}{{101}}$

Sekarang mari kita terapkan dua pengetahuan kita, kedalam soal yang lebih kompleks

Contoh 4: Hitunglah nilai dari :

$\sqrt{1+\frac{1}{1^2}+\frac{1}{2^2}}+ \sqrt{1+\frac{1}{2^2}+\frac{1}{3^2}}+\dots +\sqrt{1+\frac{1}{2003^2}+\frac{1}{2004^2}}+\sqrt{1+\frac{1}{2004^2}+\frac{1}{2005^2}}$

Jawab: Menghadapi soal seperti ini , kita mesti seneng dong

lho?

Ya iyalah, karena kita gak mungkin menjumlahkannya satu persatu.

So what ?,

itu adalah kabar baik pertama : soal ini pasti punya pola !!!! dan sebenarnya memiliki bentuk yang sederhana.

Ada lagi yang mampir di kepala sebagai asumsi awal?

Menghitung bentuk pecahan dalam tanda akar sangat sulit, so kemungkinan besar bentuk itu bisa memunculkan bentuk kuadrat sehingga menetralisir bentuk akar.

Masa sih?

Coba aja dulu, namanya juga asumsi

Proses pencarian pola:

Kita tinjau polanya: $\sqrt{1+\frac{1}{1^2}+\frac{1}{2^2}}$

Penyebut merupakan kuadrat dari dua bilangan berurutan, kita misalkan sebagai variable $x$ $\sqrt{1+\frac{1}{x^2}+\frac{1}{(x+1)^2}}$

Dari contoh 3, kita sudah tahu bentuk identitas dari pengurangan pecahan yang penyebutnya berselih satu. So…kita coba munculkan bentuk itu

$\sqrt{1+\left(\frac{1}{x}-\frac{1}{x+1}\right)^2+2. \left(\frac{1}{x}-\frac{1}{x+1}\right)}$

Karena muncul dua bentuk pengurangan sebanyak dua kali, kita misalkan saja menjadi $P$ supaya simple

$=\,\,\sqrt{1+P^2+2P}$

$=\,\,\sqrt{(P+1)^2}$

$=\,\,|P+1|$ , karena bilangan dalam tanda mutlak postif, maka tanda mutlak bisa hilang.

$=\,\,P+1$

$=\,\,\left(\frac{1}{x}-\frac{1}{x+1}\right)+1$

Sehingga soal bisa kita sederhanakan :

$=\,\,\sqrt{1+\frac{1}{1^2}+\frac{1}{2^2}}+ \sqrt{1+\frac{1}{2^2}+\frac{1}{3^2}}+\dots +\sqrt{1+\frac{1}{2003^2}+\frac{1}{2004^2}}+\sqrt{1+\frac{1}{2004^2}+\frac{1}{2005^2}}$

$=\,\, \left( 1+\frac{1}{1}-\frac{1}{2}\right)+ \left( 1+\frac{1}{2}-\frac{1}{3}\right)+\dots \left( 1+\frac{1}{2003}-\frac{1}{2004}\right)+\left( 1+\frac{1}{2004}-\frac{1}{2005}\right)$

Ternyata banyak suku yang saling menghilangkan. tinggal dihitung aja yang tersisa.

banyak angka 1 ada 2005 (pada suku pertama ada 2 buah, sedangkan pada suku lain masing-masing 1 buah)

$=\,\,2005-\frac{1}{2005}$

kalo mau disederhanakan, boleh.

$=\,\,2004+1-\frac{1}{2005}$

$=\,\,2004+\frac{2004}{2005} =2004\frac{2004}{2005}$

gimana gampangkan?

Berlatih yuk Soal 1 : (Olimpiade tingkat Kota 2003-2)

Misalkan $t_n = \frac{{n(n + 1)}}{2}$ . Tentukan jumlah dari $\frac{1}{{t_1 }} + \frac{1}{{t_2 }} + ... + \frac{1}{{t_{2002} }}$

Kunci: $\frac{2004}{2003}$

Soal 2: (Olimpiade tingkat Kota 2003)

Misalkan $a = \frac{{1^2 }}{1} + \frac{{2^2 }}{3} + \frac{{3^2 }}{5} + ... + \frac{{1001^2 }}{{2001}}$ , dan $b=\frac{{1^2 }}{3} + \frac{{2^2 }}{5} + \frac{{3^2 }}{7} + ... + \frac{{1001^2 }}{{2003}}$ Tentukan bilangan bulat yang paling dekat ke $(a - b)$

Kunci : 501

Soal 3:

Hitunglah : $\frac{1}{2} + \frac{3}{4} + \frac{5}{8} + \frac{7}{{16}} + ...$

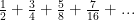
kunci : $\frac{3}{2}$

I. Menuliskan persamaan dalam beberapa baris sekaligus.

contoh 1 : $latex(x+y)(x-y) = x^2 – xy + yx – y^2 \\ = x^2 – y^2 \\ (x+y)^2 = x^2 + 2xy + y^2 $

Hasilnya:

$(x+y)(x-y) = x^2 - xy + yx - y^2 \\ = x^2 - y^2 \\ (x+y)^2 = x^2 + 2xy + y^2$

Langkah-langkah lanjutan:

Tentukan alignment dari kolom (left, center atau right)
Kasih tanda pemisah kolom dengan & symbol &

$latex\begin{array}{ccc} (x+y)(x-y) & = & x^2 – xy + yx – y^2 \\ & = & x^2 – y^2 \\ (x+y)^2 & = & x^2 + 2xy + y^2 \end{array} &fg=aa0000&s=1$

$\begin{array}{ccc} (x+y)(x-y) & = & x^2 - xy + yx -y^2 \\ & = & x^2 - y^2 \\ (x+y)^2 & = & x^2 + 2xy + y^2\end{array}$

Penjelasan:

1) Deklarasi {ccc} menunjukan ada 3 kolom dalam satu baris, (seperti dalam tabel).

kolom ke-1 diisi oleh “(x+y)(x-y)”
kolom ke-2 diisi oleh ” = “
kolom ke-3 diisi oleh ” $x^2 - xy + yx - y^2$ “

2) Setiap kolom dibatasi oleh ” &”, sama halnya dengan garis pembatas pada tabelakhir dari suatu baris ditandai dengan “// “

3). Kita bisa menggunakan alignment : c = center, l= left, r = right. sehingga {ccc} artinya : isi dari kolom ke-1 ditulis secara “center”, kolom ke-2 secara “center” dan kolom ke-3 secara “center”

Contoh 2: {lcl} artinya: ada3 kolom, dengan indentasi left, center dan left

$latex\begin{array}{lcl} z & = & a \\ f(x,y,z) & = & x + y + z \end{array} $

Hasilnya :

$\begin{array}{lcl} z & = & a \\ f(x,y,z) & = & x + y + z \end{array}$

Contoh 3: {rcr} artinya: ada3 kolom, dengan indentasi right, center dan right

$latex\begin{array}{rcr} z & = & a \\ f(x,y,z) & = & x + y + z \end{array} $

Hasilnya :

$\begin{array}{rcr} z & = & a \\ f(x,y,z) & = & x + y + z \end{array}$

Contoh 4: {rcl} artinya: ada3 kolom, dengan indentasi right, center dan left

$latex\begin{array}{rcl} f: R^3 & \to & R \\ (x,y,z) & \to & x + y + z \\ f(x,y,z) & = & x + y + z \end{array} $

Hasilnya :

$\begin{array}{rcl} f: R^3 & \to & R \\ (x,y,z) & \to & x + y + z \\ f(x,y,z) & = & x + y + z \end{array}$

Contoh 5 : {lcl} artinya: ada3 kolom, dengan indentasi left, center dan left

$latex\begin{array} {lcl} f(x) & = & (a+b)^2 \\ & = & a^2+2ab+b^2 \end{array}$

Hasilnya :

$\begin{array} {lcl} f(x) & = & (a+b)^2 \\ & = & a^2+2ab+b^2 \end{array}$

II. Case Definition

Digunakan ketika sebuah definisi memiliki dua atau lebih kasus. Perhatikan bahwa spasi setelah {if} harus dibubuhkan spasi.

Contoh 6:

$latexf(n) = \begin{cases} n/2, & \mbox{if } n\mbox{ is even} \\ 3n+1, & \mbox{if } n\mbox{ is odd} \end{cases} $

Hasilnya :

$f(n) = \begin{cases} n/2, & \mbox{if } n\mbox{ is even} \\ 3n+1, & \mbox{if } n\mbox{ is odd} \end{cases}$

III. Sistem persamaan :

Contoh 7:

$latex\begin{cases} 3x + 5y + z \\ 7x – 2y + 4z \\ -6x + 3y + 2z \end{cases} $, hasilnya:

$\begin{cases} 3x + 5y + z \\ 7x - 2y + 4z \\ -6x + 3y + 2z \end{cases}$

belajar matematika

Kamis, 14 Mei 2009

mencoba memahami matematika

Rabu, 13 Mei 2009

BILANGAN BERDERET

belajar menulis baris persamaan

facebook y2t_krentz

clock

online